Closing the loop on raw milk legislation

Earlier this year I blogged several times about raw milk and the movement advocating drinking it. One of those posts mentioned the Milk Freedom Act of 2014, a bill introduced by Rep. Thomas Massie of Kentucky, which, if passed, would have

Prohibit[ed] a federal department, agency, or court from taking any action that would prohibit, regulate, or otherwise restrict the interstate traffic of milk or a milk product that is unpasteurized and packaged for direct human consumption if such action is based solely upon a determination that because the milk or milk product is unpasteurized it is adulterated, misbranded, or otherwise in violation of federal law.

Just to circle back and check up on the status of the bill, it seems to have gone nowhere. The only echoes that came up in a quick Google search were comments attributed to Massie at a meeting called the "Food Freedom Fest" in September. The comments appear on a food rights and raw milk blog by David Gumpert:

U.S. Congressman Thomas Massie . . . was pessimistic about the chances of actually passing anything in the House of Representatives. Indeed, it isn’t even likely the legislation will get a hearing. “The dairy industry went apoplectic when we introduced the legislation,” he said. “My wife said she didn’t know the lactose industry was so intolerant.” . . . Massie told me after his talk that the best chance to get raw milk legislation through Congress and into law would be as part of some other appropriations bill guaranteed passage. Even that route is a long shot, he said, since not many appropriations bills are likely to get through in the coming year or so.

An alternate interpretation of these comments could be that a bill at odds with the basic tenants of food safety and that would place public health at risk if passed was opposed by corporations who have invested immensely in an infrastructure to deliver safe food. The only way that the bill might get passed is if it piggy backs onto a large appropriations bill, but that probably won't happen because the Congress isn't doing much these days anyway.

So, we can all rest well knowing that the Milk Freedom Act of 2014 will never see the light of day. Thank goodness for a Congress that perfected the art of doing little.

(image source: David Hartley)

An IGY for medicine

It's been an interesting first year of blogging, and I want to thank everyone for their helpful input and conversations. It's really been great.

The year 2015 will soon be upon us, bringing with it new opportunities for improving human health across a world fractured with poverty, strife, and war. Robert F Kennedy once said that

There are those that look at things the way they are, and ask why. I dream of things that never were, and ask why not.

This strikes me as an appropriate notion for healthcare and medical research. We should ask "why not?" and "what if?" much, much more often.

A little over 50 years ago an event unfolded that provided both hope for peace and a better understanding of our planet. Lasting for 18 months in 1957 and 1958, it was called the International Geophysical Year (IGY). The idea of an IGY is said to have originated in 1950, at a social gathering in James Van Allen's living room. Someone at the gathering opined that, with the recent development of tools like rockets, radar, and computers, a period of coordinated investigation could make a real impact on understanding the geosphere.

The IGY was thus an attempt to coordinate global research on, and measurements of, the earth, oceans, atmosphere, and sun. The accomplishments of the IGY were legion and included the discovery of the Van Allen radiation belts surrounding the earth; the launch of the first artificial satellites; the charting of ocean depths and ocean currents; and groundbreaking studies of the earth's magnetic field. The IGY required -- and successfully achieved -- international cooperation in a time of significant geopolitical tension. It provided a demonstration of what can be achieved when diverse peoples, who share common and coordinated goals, work together with cutting edge technologies.

Why couldn't we adapt the idea of the IGY and have a future International Biomedical Year, where nations apply tools such as supercomputing, machine learning, and genomic sequencing in a coordinated investigation of the ills plaguing human health? The idea would be to plan collaborative and complementary studies in order to accomplish agreed upon, viable steps toward solutions to important problems.

Admittedly, this is a pipe dream, but why not? What if the world's major government and non-government funding organizations closely coordinated their activities on a truly international, focused initiative? Maybe we could cure one or more cancers, or learn how to cut the incidence of heart disease, or finally understand Alzheimer's disease.

Let's try to ask "why not?" and "what if?" more often in 2015. And may you prosper and be well in the coming year.

(image source: Wikipedia)

Mumps on ice

The mumps vaccine was licensed in the US in 1967 and recommendations regarding use of the vaccine have varied since its introduction. As described in the CDC Manual for the Surveillance of Vaccine-Preventable Diseases, the Advisory Committee on Immunization Practices (ACIP)

made an official recommendation for one dose of mumps vaccine for all children at any age after 12 months in 1977. In 1989, children began receiving two doses of mumps vaccine because of the implementation of a two-dose measles vaccination policy using the combined measles, mumps, and rubella vaccine (MMR) vaccine. In 2006, a two-dose mumps vaccine policy was recommended for school-aged children, students at post high school educational institutions, healthcare personnel, and international travelers.

Mumps vaccine has had a profound impact on the annual incidence of mumps in the US. In 1968 more than 152,000 cases reported, while in 2003 only 231 cases were reported. Recently, however, the nation has witnessed a resurgence of the disease, and an apparently ongoing outbreak of mumps in the National Hockey League (NHL) illustrates how the mumps virus continues to circulate in the general population. The NHL outbreak has, so far, affected 15 players on five teams, and another three cases are suspected. A timeline of events surrounding the cases suggests the outbreak originated in October.

Doni Bloomfield wrote an article this week (which also contains "mumps on ice" in the title) that, in one vivid passage, illustrates potential infection pathways for mumps virus in professional hockey. Bloomfield quotes James Conway of the University of Wisconsin School of Medicine and Public Health:

You watch these guys taking a big hit up against the boards, there’s snot and boogers and all sorts of stuff flying around as the guy gets hit hard enough, so I don’t think it would surprise me at all that there’s some transmission just by stuff flying around during the games. It’s a sloppy, messy sport.

That's colorful imagery for sure, but in addition to how, it's important to ask why this and other recent outbreaks are occurring. Mumps is, after all, a vaccine preventable disease. 

It's possible that this group of players belongs to a demographic that has lower vaccine coverage, potentially due to parental reticence to vaccinate. However, at least one player is known to have had two doses of vaccine: one childhood dose, consistent with ACIP guidelines in the late 1980s, and another in preparation for foreign travel in February of 2014. Tara Haelle wrote an article recently on the mumps vaccine in which she quotes Paul Offit discussing the rate of waning immunity associated with this vaccine. Offit notes that

If you look at the three [MMR component] vaccines, measles and rubella induce larger memory in B and T cells . . . They have longer lasting immunity. Mumps is the weak sister of the three. You start to see vulnerability 10 years after the first dose and 10 years after the second dose.

Waning vaccine-associated immunity could thus play a role in this outbreak, and in potential future ones as well. Boosters have been used to compensate for waning immunity in past mumps outbreaks. Might a third dose of vaccine be appropriate for the general population at some point in the future?

(image source: CDC)

The epidemiology of Fearbola

In the mid-19th Century, a newspaper could reach several thousand people daily or weekly. By the mid-20th Century, TV and radio reached 10s to 100s of millions of people instantaneously and possessed a multinational reach. Today, with the Internet, and satellite TV and radio, it is possible to reach 100s of millions of people or more across the globe within minutes. This vast and practically instantaneous reach of technology feeds a seemingly insatiable, 24/7 appetite for news and information. What are the implications of this for fighting epidemics? 

We've seen some of the consequences in the Ebola outbreak this year. On the one hand, the ability of aid groups to spread information broadly has been helpful for raising awareness and bringing additional resources to bear on the epidemic. On the other hand, news headlines resulted in near-hysteria and much counterproductive behavior in the US and other developed nations. Examples were highlighted in a previous post, and many, many others have offered similar observations and commentary.

Perhaps the reactions observed in the US have been understandable, as many ingredients were present for an epidemic of sensationalism and fear: An active public imagination rooted in previous popular books and movies, a government that addressed the issue late and with almost Pollyannaish credibility at first, and a wealth of news outlets offering non-expert commentary while playing to the continuous news cycle.

The resulting epidemic of "Fearbola" should thus not be surprising. It is sobering, however, for it provides a warning for domestic public health agencies: Understand how to administer effective public health messages that are relevant and appealing to the constant clamor of CNN, Fox, and the like, or else risk being drowned out by noise and hype. What if this epidemic had been of a pathogen possessing a short serial interval and high virulence, transmissibility, and R₀? The medical system may or may not be prepared, but it seems clear that our risk communication strategies are not. Would the news coverage we saw during the Ebola hysteria in recent months have served the public well if this had been a bona fide threat to US public health?

It's important to understand how the epidemic of fear and hype came into being and propagated so well. I tend to think of messages as themselves being infectious. From that perspective, the ideas that resulted in the hysteria surely had R₀ > 1. For ideas related to "dread threats", such as virulent infections with no known cure, is this unavoidable given the high contact rate (e.g., frequency of checking for news and rumors combined with near-constant coverage), short serial internal (e.g., rush to post on social media), broad coverage, and rapid dissemination of modern communications?

If so, we must learn how to craft public health messaging strategies so that authoritative messages will out-compete hype and fear in our hyper-connected world. If we don't learn how to do so, we run the risk that important messages will be drowned out by high-incidence, fearful messages in future outbreaks of international public health importance.

(image source: David Hartley)

Ebola: Encouraging news but far from victory

Recent statistics from West Africa suggest that the epidemic of Ebola virus disease is declining in some areas. While this is welcomed and good news, it's important to remind ourselves that the public health emergency is not over and that significant uncertainties remain. Dr. Joanne Liu, the current president of MSF, described the reasons in an interview with Julia Belluz:

Strictly speaking, when we look at our figures, there is deceleration in the number of cases in a few spots in Liberia and Guinea, but they are still on the rise in Sierra Leone.

There are a few things we need to be conscious about: we have had those decelerations in the past. Basically, it happened while it was spreading in other communities and after that, there was another surge in other hot spots. So we need to make sure it’s an opportunity to consolidate our Ebola isolation centers and case management, strengthen the community information and education. That is key. We need to use this time for that. But the main thing is to not let down our guard.

There’s no room for complacency, no room for mistakes. Every time you go down that path, you pay: you get infected, more people are infected. Ebola does not allow you to make mistakes.

This is certainly true. I think it's also a critical time in another way: With the medical aid in the region and the momentum it is gaining, it would be a shame not to begin asking what will happen when the epidemic is finally conquered. Will the international community simply pull out, leaving a vacuum made more acute by the scores of local healthcare workers lost to Ebola itself? Or, is there a way that the current activity could bolster and influence medicine and public health there for years to come? Some ideas may be creeping into the conversation: US and Liberian officials have decided to reduce the number of Ebola treatment units planned and are discussing spending the money saved on programs aimed at combating future epidemics.

For now, however, we must avoid complacency and remain committed to providing the resources needed to fight the ongoing epidemic. I don't think it's too early to begin conceiving a foundation for improving regional medical and public health capabilities more broadly, however. Perhaps some of the capabilities on site in the affected areas now can be transitioned into a sustainable, effective medical and public health presence at the appropriate time. Not doing so would be a missed opportunity.

(image source: USAID/ Carol Han)

Influenza vaccine recommendations: Stop needling me!

Seasonal influenza is responsible for an estimated 200,000 hospitalizations and 23,000 deaths in the US annually. Each year influenza vaccines are produced based on the viruses forecast to become prevalent. There are two types of vaccine: inactivated influenza vaccine (IIV), delivered via injection, and live attenuated influenza vaccine (LAIV), delivered via a mist sprayed into the nose. Influenza vaccines typically have efficacies exceeding 60% and an estimated 46% of the American public relieves vaccine annually.

While many people are vaccinated each year, it is desirable to increase vaccination rates for at least two reasons. First, vaccine-associated immunity protects individuals from developing potentially serious or fatal disease. Second, high population coverage produces a herd immunity effect: those possessing vaccine-associated immunity cannot become infected and thus cannot infect others. This is especially important for protecting individuals for whom vaccines are contraindicated.

Individuals who are immunocompromised or immunosuppressed are such a group. Consider, for example, patients recovering from hematopoietic stem cell transplantation (HSCT) following myeloablative conditioning. In cases of imperfect donor-recipient match, patients may take immunosuppressive medications as prophylaxis against, or treatment for, graft versus host disease. During this process of immunologic tolerization, which can last months or longer, patients must avoid crowds and limit work/school and social interactions in order to avoid potentially fatal infections. And during this period it is critically important for caregivers and contacts to be vaccinated against influenza and other vaccine-preventable diseases so that they do not become infectious.

LAIV is contraindicated for caregivers of such persons in the Advisory Committee on Immunization Practices (ACIP) guidelines. Because LAIV contains live influenza viruses, a potential exists for transmission of vaccine strain viruses from vaccinees to other persons. The period of viral shedding in vaccinees is variable and relatively short lived. Vaccinated immunocompetent children, for example, shed vaccine viruses for less than 3 weeks, and evidence suggests that shedding may be much shorter lived than that. LAIV-associated shedding occurs in lower titers than is typically observed in disease-associated shedding caused by wild-type influenza viruses.

As several studies have demonstrated higher efficacy of LAIV relative to IIV in children (but see the footnote below), the ACIP has expressed

a preference for the use, when immediately available, of live attenuated influenza vaccine (LAIV) for healthy children aged 2 through 8 years, to be implemented as feasible for the 2014–15 season but not later than the 2015–16 season.

Higher protective efficacy of LAIV in children provides strong rationale for the ACIP statement. Moreover, promoting LAIV as an alternative to IIV in older patient populations may result in increased coverage in those who avoid vaccination due to fear of needles. I wonder if increased use of LAIV might pose additional risk to immunocompromised persons, however, in terms of inadvertent exposure to recent vaccinees shedding live, though attenuated, influenza viruses. Such patients may need to become more meticulous in screening visitors and contacts who may have received LAIV recently.

Footnote: During 2013-2014 there was no measurable effectiveness for LAIV against influenza A (H1N1) among children enrolled in effectiveness studies. The reasons for this are unclear.

(image source: Wikipedia)

Planning for the unplannable: What about next time?

A recent article in Forbes, written by Scott Gottlieb, began by observing that

The response by public health officials and local providers to the first case of Ebola diagnosed on U.S. soil has been marked by some tragic missteps. Mistakes have resulted in the avoidable secondary spread of the infection to healthcare workers. This is an appalling outcome to a crisis . . . But, sadly, it should neither be surprising, nor foretell a future marked by continued blunders.

As he suggests, I'd really like to think that the response to the events in Dallas will result in better ED and hospital care. It's important to learn from errors, and this seems to be happening: There's been a dramatic increase in infection control awareness since late September.

That seems like a good thing, but there's more to the picture. Alison Bruzek wrote an interesting piece for NPR last week on how, for hospitals, doing more on Ebola can mean less elsewhere. A passage from the article illustrates the point:

For infection preventionists, a normal routine includes "Looking at the lab results[.] [W]e're looking at what new patients maybe came onto a unit, we're taking calls from the unit, [and answering questions like] 'What do you think I should do about this particular thing?'" says Linda Greene, an infection prevention manager and member of APIC's regulatory review panel. But now, Green says, if the infection preventionist is working on training with personal protective equipment for Ebola, their other tasks aren't getting done as promptly or efficiently as they could be. As a result, Greene [says] the fear is that they'll "miss red flags" for patients with the flu or antibiotic-resistant bacteria.

How can this be avoided? It's difficult for many reasons, including that hospitals, financially speaking, are zero sum propositions: Annual budgets govern allowances for departments. A previous blog discussed the trade off between different infection prevention activities given a constant budget through a fictional story. Bruzek's article highlights how focus here might lead to shortcomings there, all things being equal (i.e., budgets and resources being constant), in a real situation.

One might think that hospitals should simply do a better job of planning for contingencies like the Ebola preparations in which they are now engaged. Perhaps they could, but it's not necessarily simple; budgetary contingencies are usually for things that are random but can be conceived and planned for. Nobody forecast this Ebola event or the implications for US healthcare, and no hospital could rightly be expected to have included Ebola preparations in their fiscal year planning.

Moreover, this situation may have been unplannable. While analyses of public health threats, including bioterrorism, have considered a broad range of issues, I don't have the sense that anyone truly anticipated the extent of the hospital, media, or political issues encountered in the US recently. Nonetheless, the need to prepare for complex unexpected events cannot be denied.

So how do we plan for the unplannable? To address the issues mentioned in Bruzek's article would require specialized human resources and the funds to engage them on a surge basis, in addition to money for PPE. Planning for the availability of such human, material, and financial resources is not easy when they are required randomly, rarely, and -- as in this case -- widely. It's important for public health researchers, professional organizations, and trade groups to study and address such issues, because if there's one thing nature has taught us, it is that there will be a next time.

Fearbola

Some people in the US have absolutely panicked over the threat of Ebola at home. To cite but a few examples:

• A Portland, Oregon, high school canceled a visit by African students, citing concerns about Ebola. The 18 visiting students came from Republic of Congo, Niger and Ivory Coast, none of which currently have reported cases of Ebola, according to the WHO.
• Two children who recently moved to the US from Rwanda are being kept home from school after parents at an elementary school in New Jersey voiced concerns. Rwanda is in East Africa, over 2,500 miles from the West African areas where Ebola virus is currently circulating.
• An assistant principal at a North Carolina middle school has to spend 21 days working from home when she returns from a mission trip to South Africa, by order of the school board. The chairperson of the school board explained why: "It’s not that we think that she poses any type of risk, but it's public perception here that we're concerned about.

More examples are described in a recent CNN article, which also notes that:

This is getting ridiculous. While the threat of Ebola is very real in Africa, the paranoia it's generated in the United States is unreal.

Many baseless actions are being taken out of "an abundance of caution", and it's not only in the US: A recent article by Andrew Higgins describes similar behavior in Europe.

While listening to the radio while working today, it struck me how someone having a case of air sickness on a commercial jetliner now makes the national news. Perception of risk is a notoriously sticky subject, but perhaps it's a good time to begin a conversation on how to educate people better on the topic. Could some basic elements of risk assessment be taught, for example, in high school?

(image source: Wikipedia)

Fear, Ebola, and the plague doctor's outfit

An earlier post mused that, in some ways, modern healthcare workers in contact precautions might appear as the plague doctors did in the Middle Ages to their febrile, terrified patients. The imagery of the plague doctor's outfit has survived centuries in association with a horrific event responsible for significant death and social disruption. Today, the doctor's outfit remains a powerful symbol of desperate times.

While the current epidemic of Ebola virus disease is unlikely to have the depopulating effect that plague did in the 1300s -- the Black Death is estimated to have killed up to 60% of the European population at the time -- the deadliness of this virus as it circulates in Western Africa must produce a fear similar to that of the Black Death in the Middle Ages. It makes me wonder if, years from now, pictures of doctors and nurses in Ebola personal protective equipment (PPE) -- the garb healthcare workers must wear to care for patients -- will conjure up similar reactions to those of the plague doctor's outfit.

Think of the similarities. If the case fatality rate (CFR) of plague in the 14th Century was similar to that of plague in the US between 1900 and 1941 (i.e., in the pre-antibiotic era), the CFR of the Black Death could have been over 60%. The CFR of Ebola in West Africa is currently estimated to be near 70%. Probably due to this high CFR during the Black Death, people were often deeply skeptical of doctors, as as Giovanni Boccaccio  describes in The Decameron:

Which maladies seemed set entirely at naught both the art of the physician and the virtue of physic; indeed, whether it was that the disorder was of a nature to defy such treatment, or that the physicians were at fault - besides the qualified there was now a multitude both of men and of women who practiced without having received the slightest tincture of medical science - and, being in ignorance of its source, failed to apply the proper remedies; in either case, not merely were those that covered few, but almost all within three days from the appearance of the said symptoms, sooner or later, died, and in most cases without any fever or other attendant malady . . . 

As we have read in this event, distrust of healthcare workers in Western Africa has led to attacks on doctors, though this sentiment may partially stem from historical events. Indeed, serious issues with healthcare in this region are nothing new.

Of course, there are important differences between bubonic plague in the Middle Ages and Ebola in Africa today as well. Plague is caused by a bacterium whereas Ebola virus disease has a viral etiology; Yersinia pestis is carried by domestic rodents and vectored to humans by fleas whereas Ebola virus is directly transmitted between humans; et cetera. Perception is reality, however, and one overarching public perception is proving a difficult to alter: Ebola is terrifying. Ebola PPE is a modern plague doctor's suit, a tangible symbol of fear, a fear that we have but to turn on any newscast to see spread.

I feel strongly that we must never forget the human dimensions of disease. Physiologically speaking, Ebola virus disease in Homo sapiens is increasingly well understood, but the impact of the disease on the human condition is perhaps less so. If we are to control the spread of Ebola virus, we must understand this better; it seems clear that we don't. Fear and panic only make the situation worse. We must control the fear.

(image source: Wikipedia and WHO)

Ebola versus influenza and some thoughts on screening

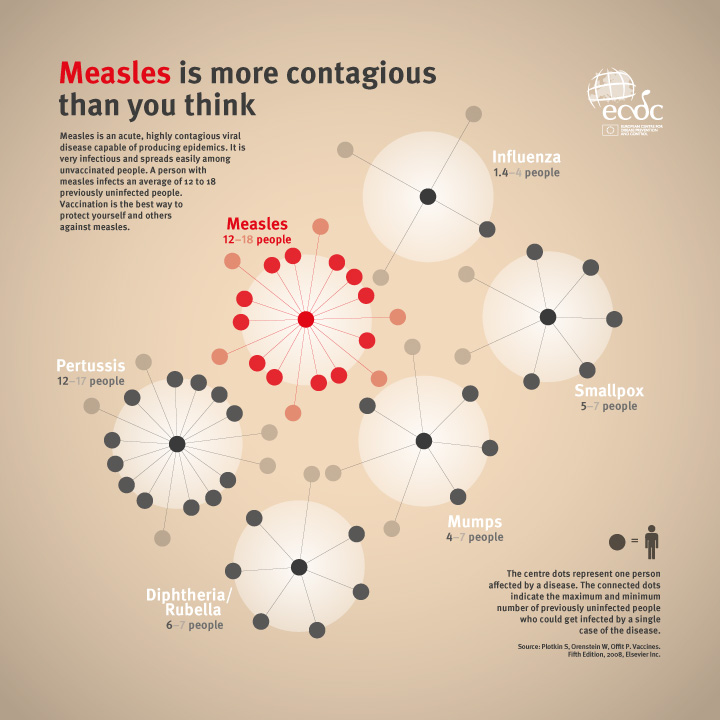
My colleague Eli Perencevich wrote an interesting blog this week in which he discusses airport screening. He points out that some of the discussion surrounding travel restrictions and Ebola are related to ideas from (and models of) epidemics of respiratory viruses, including the 2009 H1N1 pandemic. In the post he highlights some of the important differences between Ebola and influenza:

. . . Ebola is slower moving, has a much longer incubation period (especially compared to the duration of a transcontinental flight), and is not contagious before symptoms develop. What does this mean? It means that if Ebola was as infectious as influenza, millions would have already died - apocalypse. It also means that since Ebola is not transmissible during its long incubation period, it may be possible to quickly isolate patients when symptoms develop. Thus, airport screening on exit or entry could limit transmission and perhaps through early diagnosis allow Ebola infected patients to receive life saving treatment more quickly. 

Later in the post he highlights the need for mathematical model-based analysis of the impact of specific Ebola screening programs. I recommend reading the blog.

As I mentioned in a comment to the piece, in addition to incubation period, it's useful to consider the serial interval (the period between infection and transmission; sometimes also referred to as the generation interval or generation time) and basic reproduction ratio (R₀). As discussed before, estimates for R₀ for Ebola in this event are similar to estimates of R₀ for pandemic influenza events. White and Pagano estimate the serial interval for a 1995 outbreak of Ebola in Congo to be 5.4-7.6 days and the WHO Ebola Response Team estimates the serial interval for the current epidemic to be near 15 days. By comparison, estimates of the serial interval for the 2009 pandemic of influenza fall in the range of 2.5-3.0 days. Ebola has much longer serial intervals than does influenza.

What do we take away from this? One thing is that the serial interval is important for understanding the speed of spread. Perencevich observes that

. . . the first case of Ebola is thought to have occurred 307 days ago on December 6th in a two-year old boy. Since that time there have been an estimated 8,032 cases (granted these could be underestimates). If you compare a similar 307-day period for 2009 H1N1, April 12, 2009 to February 12, 2010 CDC estimated that between 42 million and 86 million cases occurred in the US with a mid-level estimate of 59 million people infected. Think about that -- 7,300 times more cases of H1N1 using the mid-level estimate during the same 307 days.

It's clear, then, that equating influenza and Ebola on the basis of R₀ alone is misleading. Thinking of R₀ as a reproductive factor for each generation of infection (at the beginning of an epidemic in a susceptible population) and the serial interval as how rapidly generations of infection occur, however, it becomes clearer that the much shorter serial interval of influenza is related the explosive emergence of influenza cases in 2009-10 relative to Ebola in 2013-14, despite the similar R₀ values. It's more complex than this in reality; Wallinga and Lipsitch present a detailed mathematical treatment of how generation intervals shape the relationship between epidemic growth rates and reproductive numbers, and Lipsitch et al illustrate, within the context of SARS, how incubation period, serial interval, and epidemic growth rate combine to produce estimates of R₀.

Another thing to ponder is that longer serial intervals can, depending on the length of the incubation period, give more time to institute control measures. On the one hand, the long serial interval relative to incubation period in the case of Ebola may suggest a higher likelihood of detecting an infectious traveler in an airport than there is for influenza. On the other hand, the extremely low incidence of Ebola in passengers must also be considered; it may not be an efficient activity to devote resources to.

I agree with Eli that mathematical models can help shed light on such questions. Perhaps such models have been published, I admit to falling behind on the mathematical epidemiology of Ebola results in the last two weeks. 

(image source: David Hartley)

Ebola, EHRs, and the difficulty of communication

A quick update to a point discussed in the last post. On Thursday night, the Dallas hospital treating the patient suffering from Ebola virus disease explained the mix-up over his travel history. A news release on the hospital's website reads:

10/02/2014
 . . . Protocols were followed by both the physician and the nurses. However, we have identified a flaw in the way the physician and nursing portions of our electronic health records (EHR) interacted in this specific case. In our electronic health records, there are separate physician and nursing workflows.

The release then explained that the flaw had been remedied, by relocating the "travel history documentation to a portion of the EHR that is part of both workflows" and to "specifically reference Ebola-endemic regions in Africa".

The promptness of the communication was reassuring and helpful, and suggested that an analysis of the situation had been undertaken promptly, a cause of the error identified, and action taken to fix it. But 24 hours after the news release, a perplexing clarification was posted:

10/03/2014
We would like to clarify a point made in the statement released earlier in the week. As a standard part of the nursing process, the patient's travel history was documented and available to the full care team in the electronic health record (EHR), including within the physician’s workflow.

There was no flaw in the EHR in the way the physician and nursing portions interacted related to this event.

It's difficult to interpret the dissonance of these two releases, and I think they highlight a hugely important in hospital care: the challenges of effective communication between all members of the healthcare team.

Joyce Frieden wrote a very nice essay on the Dallas episode (published before the hospital's "clarification"), which I recommend reading. One passage describes some of the challenges to effective communication in the clinic:

Although the EHR could have been configured to import the nursing notes -- or at least their key items -- into doctor's notes automatically, "I'm sure some doctors would say it would be a bad idea because it would fill their notes with stuff they're not interested in," he [Dr Dean Sittig] continued. "So that's the culture of the two professions not respecting what each profession does. Whereas before docs had to flip through the nurse's notes to get to where they wanted, now they're on a separate tab. The flaw was that they weren't pushed into the doctor's face."

The importance of effective communication, from the perspective of the Magnet® process, has been discussed by Swanson and Tidwell, who note that 

One characteristic of exemplary professional practice is meticulous attention to communication processes. . . . This use of SBAR has created a standardized approach to information sharing. It has created a shared mental model for effective information transfer by providing a standardized structure for concise, factual communication among clinicians, whether it is nurse-to-nurse, doctor-to–doctor, or nurse-to-doctor communication. It is now used to ensure that patient information is consistently and accurately communicated, especially during critical events, shift handoffs, and patient transfers between levels of care. [Emphasis added.]

Apparently this critical nurse-doctor communication and information transfer didn't occur during the patient's hospital visit on September 26th.

Effective communication is a human process. Software should be used to improve that process, not replace it.

(image source: David Hartley)

Ebola and the cult of vitamin R

This week saw the appearance of Ebola virus disease in a Liberian visitor to the United States. Active transmission here is not expected and public health authorities have done extensive contract tracing. Fifty individuals who were potentially exposed to the virus are being monitored and a small number are in isolation. 

First, a brief description of the episode. A man who had direct contact on September 15th with a woman suffering from advanced Ebola virus disease in Monrovia, Liberia, traveled to Dallas, Texas, to visit relatives. He flew from Monrovia to Brussels on the 19th of September and took a connecting flight to Washington DC before catching a final flight to Dallas, arriving on the 20th. He was screened for fever and exposure at the airport before departing Liberia; apparently, his answers to a screening questionnaire were inaccurate. After arriving in Dallas he remained asymptomatic for several days and began suffering symptoms on the 24th. On the 26th he presented to the hospital. (Note: some news accounts report the date as the 25th.) At this first visit he was evaluated, prescribed antibiotics, and sent home to the relatives with whom he was staying in Dallas. He subsequently deteriorated and was transported to the ED by ambulance on the 28th. The positive test for Ebola virus was received on the 30th.

Many details about this event are unsettling. To me, especially disappointing is that the man's travel history was not a factor in the clinical diagnosis on the 26th, although a nurse was informed that he was visiting from Liberia. The nurse entered the information into the electronic health record (EHR), following protocol, but that didn't trigger suspicion. The hospital has since clarified why: There are separate physician and nursing workflows, and patient travel history did not automatically appear in the physician's standard workflow. The doctor never saw the information.

I think it's also interesting that the man was prescribed antibiotics for what turned out to be a viral illness. In a sense, this is a familiar story: change the name of the virus and it's a scene that occurs daily in many clinics and office visits. It seems ironic that, a week after the White House released its National Strategy for Combating Antibiotic-resistant Bacteria, this physician-patient encounter resulted in the apparent inappropriate prescription of antibiotics. As the National Strategy tells us, 

. . . a growing body of evidence demonstrates that programs dedicated to improving antibiotic use, known as "antibiotic stewardship" programs, can help slow the emergence of resistance while optimizing treatment and minimizing costs. These programs help providers prescribe the right antibiotic for the right amount of time and prevent prescription of antibiotics for non-bacterial infections. It is imperative that such programs become a routine and robust component of healthcare delivery in the United States. (emphasis added)

To be fair, the man may have had a bacterial infection at the first hospital visit, in addition to the unsuspected Ebola virus infection. We don't know; it's a matter of his private health record. However, I am reminded of how a physician colleague once described the pervasive inappropriate, and often rushed, use of antibiotics,

It's a common problem. Patients present with vague complaints that are plausibly due to bacterial infection and there is a very low threshold for prescribing antibiotics. The patients often request or insist on it, and it often seems harmless to acquiesce. In fact, many doctors view prescribing them as a protection mechanism in case there is an infection or one develops. It's so common that in many clinics and EDs ceftriaxone is referred to as "vitamin R".

Perhaps the antibiotic prescription dimension of the encounter on the 26th is all too understandable.

One can hope that a thorough, transparent investigation and analysis of this entire episode can produce helpful knowledge on how to harden healthcare systems for routine healthcare as well as extraordinary events like this one. In the meantime, the CDC has produced clear guidance for evaluating patients with a history of traveling to epidemic regions.

Acknowledgement: The title is inspired from a Medscape Connect item entitled "The cult of Vitamin R", which no longer appears to be available online.

(image source: Wikipedia)

Epidemiology and behavior in the time of Ebola

This week the WHO Ebola Response Team published a paper raising the notion that Ebola could become endemic in the human population of West Africa. The idea hadn't occurred to me previously, and it struck me as very unlikely. After all, this is a directly transmissible disease that, as many have told us, we know how to control.

After reflecting on the possibility, however, I don't think it can be discounted out of hand. On the one hand, breaking the chain of transmission can be achieved theoretically with careful attention to infection control and prevention practice, which is well defined in the healthcare environment. On the other hand, this isn't a nosocomial outbreak. Community transmission is the major driver of incident cases, so changing human behavior in the community must occur if this epidemic is to be stopped. In general behavior is hard to affect, and in this case it may be even harder, given recent descriptions of distrust between healthcare providers and the community.

As I've mentioned before, one of the uses of mathematical modeling is to support clear and careful thinking. In this case, epidemiologists have applied models to estimate the basic reproduction ratio, R₀, and have found it to be greater than 1, consistent with estimates from past outbreaks. Such an R₀ suggests that the virus has the potential to circulate permanently in the human population at some non-zero endemic prevalence. Endemic prevalence levels could be, relatively speaking, high or low (or intermediate). If low enough, the disease could fade out stochastically on its own, but at higher prevalences the continual danger of sporadic cases could persist indefinitely. Models can help us gain a sense of the relative likelihood of such outcomes.

The risk factors for acquiring Ebola virus infection are well known. If effective interventions reducing risky behavior are instituted widely and adhered to, they may reduce the effective reproduction ratio, R_eff, to less than 1, thereby breaking the chain of transmission. Achieving that must entail not only nosocomial infection control but also infection prevention through behavioral change in the community.

Changing behavior surely involves building and rebuilding trust between healthcare providers and local people. I suspect and hope that the recent massive pledges of, and plans for, assistance will help build the necessary rapport and trust. Maybe the construction of clinic facilities that better support effective care will help advance such endeavors. One thing is certain, however: the longer those pledges take to become reality, the more likely the worst scenarios for the course of this epidemic become.

(image source: Wikipedia)

Ebola: Mutation, selection, and all that

The New York Times recently published an op-ed on the Ebola situation in western Africa. One of the things discussed by Michael Osterholmn in that essay is the possibility that "an Ebola virus could mutate to become transmissible through the air." I think this is an interesting idea; if the currently circulating virus were to become dramatically more transmissible, it would make an already desperate situation dire.

The issue of mutation and selection is complex, as described in an excellent post by Jamie Jones. What selective pressures are acting upon Ebola viruses circulating in western Africa currently, and how those might alter the clinical epidemiology of the disease, are interesting and relevant questions.

Many have reacted to the question of how real the risk described by Osterholm is. I think positing such possibilities, and the ensuing discussion, is helpful. Even if the possibility is a false alarm, having people think through the issue, likelihood, and potential impact has value. It should not, however, distract us from important and desperately needed public health operations on the ground, or advocacy efforts to increase the resources for those operations.

(image source: Wikipedia)

On truthiness, celebrities, and math

Katy Waldman recently published an article discussing how people's minds tend to grasp at the "low-hanging cognitive fruit" in daily life. She describes how sometimes we accept ideas as facts according their "truthiness" (a term coined by Steven Colbert in 2005). It's an interesting article and I recommend reading it. It makes me wonder about the role of truthiness in health-related behavior.

Colbert has described the notion of truthiness:

It used to be, everyone was entitled to their own opinion, but not their own facts. But that's not the case anymore. Facts matter not at all. Perception is everything. It's certainty. . . . Truthiness is "What I say is right, and [nothing] anyone else says could possibly be true." It's not only that I feel it to be true, but that I feel it to be true. There's not only an emotional quality, but there's a selfish quality.

Waldman surveys some of the evidence for truthiness: how people, instead of analyzing data critically to draw conclusions, sometimes accept ideas based on seemingly unrelated criteria, like the aesthetic presentation of a written message or the familiarity of a message bearer's name.

Within the realm of health behavior, truthiness can be devastating. In epidemiology, for example, it is often said that people who suffer from a condition tend to look for and find a cause, whether one exists or not. Truthiness reminds me of Jenny McCarthy's views on vaccination and autism, which she described during an interview on The Oprah Winfrey Show:

Winfrey: So what do you think triggered the autism [in your son]? I know you have a theory.
McCarthy: I do have a theory.
Winfrey: Mom instinct.
McCarthy: Mommy instinct. You know, everyone knows the stats, which being one in one hundred and fifty children have autism.
Winfrey: It used to be one in ten thousand.
McCarthy: And, you know, what I have to say is this: What number does it have to be? What number will it take for people just to start listening to what the mothers of children who have autism have been saying for years? Which is that we vaccinated our baby and something happened. . . .
McCarthy: Right before his MMR shot, I said to the doctor, I have a very bad feeling about this shot. This is the autism shot, isn’t it? And he said, “No, that is ridiculous. It is a mother’s desperate attempt to blame something on autism.” And he swore at me. . . . And not soon thereafter, I noticed that change in the pictures: Boom! Soul, gone from his eyes.

The post hoc, ergo propter hoc fallacy of the passage has a high truthiness to many, even though scientific bodies have debunked the notion that vaccination causes autism.

How do "truthy" fringe ideas persist and grow in the general population? Deffuant and coworkers in 2002 published a study applying agent-based modeling to analyze the propagation of extremist views. Nigel Gilbert's book describes the study succinctly:

In Duffuant et al's model, agents [individuals] have an opinion . . . and a degree of doubt about their opinion, called uncertainty . . . An agent's opinion segment is defined as the band centered on the agent's opinion, spreading to the right and left by the agent's value for uncertainty. Agents interact randomly. When they meet, one agent may influence the other if their opinion segments overlap. If the opinion segments do not overlap, the agents are assumed to be so different in the opinions that they have no chance of influencing each other. If an agent does influence another, the opinion of one agent (j) is affected by the opinion of another agent (i) by an amount proportional to the difference between their opinions, multiplied by the amount of overlap divided by agent i's uncertainty minus one. The effect of this formula is that very uncertain agents influence other agents less than those that are certain.

 . . . The model shows that a few extremists with opinions that are not open to influence from other agents can have a dramatic effect on the opinions of the majority . . .

In the case of vaccination and autism, the high truthiness (to some) of the idea that MMR vaccine causes autism produces a group of people very certain in their beliefs. Duffuant et al, working within the context of political ideas, show that such a group can impact the opinions of others, thereby propagating their ideas.

Perhaps similar dynamics apply to the case of vaccination, and potentially other health-related memes such as the raw milk movement. I also wonder about the truthiness of the local myths surrounding Ebola and how those might spread more widely, potentially affecting public health in outbreak areas adversely.

(image source: Wikipedia)

Why model infectious disease: Ebola

Several weeks ago I wrote a blog on why modeling infectious disease is useful. Now seems like a good time to highlight a few issues regarding "why model?" within the context of the current Ebola event. Science Insider recently published a very nice piece on Ebola modeling and some initial results from different groups working the issue. Discussing the article with a few colleagues who are not modelers, however, I sensed some skepticism regarding the past track record of models and why it's useful to model this outbreak.

As described by many authors previously (see the links in the previous blog), a major use of modeling is to help researchers think carefully about a problem. That's especially true in the current situation, where models can help analyze complex issues. A few examples include:

• What can be derived from data in hand, or data that can be collected, to improve our ability to clarify the situation? 
• Can we infer how quickly the virus is being transmitted and whether it is decreasing, increasing, or staying the same (questions regarding the basic reproduction ratio, R₀, and the effective reproduction ratio, R_eff)?  
• If vaccines become available, what coverage and efficacy might be necessary to control the outbreak (i.e., reduce R_eff below 1)? What vaccination strategies are likely to make optimal use of resources?
• Are there combination interventions that might prove effective at reducing the incidence of infection? 
• What is the likelihood of Ebola cases arriving in distant nations via air travel? 

In short, there are plenty of questions that modeling can help elucidate.

One should be skeptical about any epidemiologic method, including mathematical and computer modeling, when the stakes for public health are so high. Ultimately, however, policymakers need timely and defensible analytic guidance to support allocation of scarce resources. Modeling is one component of such guidance.

(image source: David Hartley)

Nowhere is it written that dangerous pathogens must have high basic reproduction ratios

As discussed previously, there are lessons aplenty to learn from the ongoing Ebola outbreak in West Africa. One simple lesson is this: Even with a low basic reproduction ratio (symbolized mathematically as R₀), a pathogen can still spread widely under the right conditions.

Current estimates of the basic reproduction number for this Ebola outbreak are roughly in the range of 1.3-2.5. That's pretty modest when compared with other notorious agents. Estimates of R₀ for smallpox outbreaks, for example, were typically 4-10 and those for cholera epidemics can be in the range of 3-12. Measles outbreaks can have R₀ values of up to 18.

R₀ itself is sometimes thought of as a surrogate for "epidemic potential". Certainly, and by definition, pathogens with high R₀ spread quickly, whereas pathogens with lower R₀ don't. Does this mean that pathogens possessing relatively low values of R₀ have lower potential to harm public health?

Certainly not. In fact, pandemic influenza viruses, for example, often fall in the range 1.5-2.0. Pathogens associated with lower values of R₀ can spread widely if control efforts are not effective. In the case of pandemic influenza, control measures include vaccination and handwashing. In the current Ebola situation, due to a range of social, economic, and political factors, it has been difficult to implement widespread, effective control measures. The infection has thus spread and will likely continue do so in the region.

Does this have implications for other infections? It absolutely does. One could imagine some theoretical pathogen, for example, that is spread predominantly by hands (call it "pathogen X") and that is not killed by alcohol based hand rub (ABHR). Then, in circumstances where ABHRs are used in place of handwashing, one might imagine that pathogen X could, over time, become widely prevalent, even if it does not possess a high R₀. Pathogen X might be similar to Clostridium difficile; one estimate of R₀ for C. difficile is in the range 0.5-1.5.

For this reason, we should not think only in terms of R₀ for classifying pathogens as dangerous or not. While high R₀ pathogens spread quickly, leaving little time to react and take action, Ebola in West Africa this year demonstrates that a pathogen possessing a more modest R₀ can result in a dangerous public health situation. 

There's a story, which is possibly apocryphal, that Enrico Fermi once remarked that nowhere is it written that the laws of physics must be linear. I think there's an analogue that should be kept in mind in infectious disease epidemiology: Nowhere is it written that dangerous pathogens must have high R₀.

(image source: ECDC) 

Outbreaks and do-overs

The current Ebola outbreak in Western Africa has been remarkable in terms of the number of cases and deaths; length and geographic extent of the outbreak; and its designation as a public health emergency of international concern. What could have been done differently to change the course of events? Thorough analyses of the outbreak and response will be done, and that will take time, but I think there are several things to consider.

More international assistance early in the outbreak. Early intervention is a mantra of modern medicine and public health, and indeed organizations like MSF and others brought impressive resources to bear early in the outbreak. Yet, transmission wasn't controlled and the epidemic grew. More resources are needed urgently. In hindsight, greater multilateral international aid earlier in the outbreak was needed, but how can nations know when NGO efforts need supplemental resources? Perhaps studying the early phases of this outbreak can suggest a way.

Better communication. The social disruption evident in this event is painfully clear and may have been intensified by the difficulty of communicating important public health messages. Anecdotes of healthcare workers being attacked and of disbelief that Ebola virus even exists are but two examples.

Balanced communications in the United States was mixed. On the one hand, many valid messages were circulated, including that Ebola poses little risk to the US general population. On the other hand, one expert told Congress that

We know how to stop Ebola with strict infection control practices, which are already in widespread use in American hospitals, and by stopping it at the source in Africa.

The second part of the statement is true enough: stopping an outbreak before it spreads is canonical in public health. However, the first part of the statement implies that strict infection control practice can prevent infection of healthcare workers and others in a hospital. That's a little problematic. If that were so, there wouldn't be problems with hospital-associated infection in the US.

By that calculus, for example, the 2011 outbreak of KPC-producing Klebsiella pneumoniae at the NIH shouldn't have occurred -- and yet the infection control practice in that event was meticulous from the initial presentation of the patient at the facility. What if an Ebola patient isn't recognized immediately when presenting at a US emergency department? And if a case is recognized, is infection control as it is actually carried out in practice likely to be effective? Such questions apply to any nosocomial pathogen, and I think it's important to ask: Given that KPC escaped a patient's room even with full precautions, why not Ebola?

Drug therapy. There are no approved treatments for, or vaccines against, Ebola virus infection. The development of new drugs is a scientifically, economically, and politically complex activity. The urgent need for new antibiotics, for example, has been discussed in connection with a large and growing need. The CDC recently reported that

Each year in the United States, at least 2 million people become infected with bacteria that are resistant to antibiotics and at least 23,000 people die each year as a direct result of these infections. Many more people die from other conditions that were complicated by an antibiotic-resistant infection. 

That's a massive burden of disease compared to the Ebola outbreak at present. Every case of any infection deserves effective management, but where is the incentive for drug development for Ebola and other exotic, low incidence infections? It is literally taking on act of Congress to help spur new antibiotic drug development in the US. Clearly drug therapies for Ebola would have been beneficial in this outbreak, and how to incentivize development seems an important question. In the absence of effective therapies and drug regimens, misinformation about bogus cures inevitably spreads and requires time and resources to counter.

Certainly these and related issues will be discussed and studied in depth in the coming months and years. Answers to the question of what could we do better next time must be found, because there will be future outbreaks of virulent emerging infections. How will we react?

(image source: CDC) 

Hepatitis in the summer of '69

A remarkable epidemic took place in 1969 at the College of the Holy Cross in Worcester, Massachusetts. In the autumn of that year, the college was forced to cancel the football season after the first two games due to an outbreak of hepatitis. 

The first football game of that season was against Harvard and took place on September 27th; Holy Cross lost 13-0. The team appeared sluggish to fans, and one player missed the game due to fever. Michael Neagle described what happened next in a 2004 essay:

Players began dropping out during the week leading up to the team’s next game at Dartmouth [on October 4th]. What had been described as a “flu bug” by newspapers during the week was confirmed as hepatitis the day of the game. Eight players did not make the trip because of illness. Some got sick on the drive up. More were sidelined when they fell ill during the game . . .

Holy Cross lost 38-6. There were interesting facets to this outbreak, as told in a 1972 Associated Press story:

The outbreak was somewhat puzzling because faculty members, the freshman football team, and others on the Worcester, Mass., campus before formal opening of classes were not affected. Food services were studied and did not produce suspicious leads.

Neagle describes what was eventually pieced together:

. . . [the] season was doomed after just the second day of practice. On Aug. 29, a hot summer day in Worcester, on the practice fields where the Hart Center now stands, players drank water from a faucet that was later found to be contaminated with hepatitis. Though investigators almost immediately suspected the drinking fountain as the source of the illness, it took nearly a year to determine conclusively the sequence of events that led to the contamination.

On that fateful day, firefighters battled a blaze on nearby Cambridge Street. This caused a drop in the water pressure, allowing ground water to seep into the practice field’s irrigation system. That ground water had been contaminated by a group of children living near the practice facility who were already infected with hepatitis. Once the players drank from the contaminated faucet, they too became infected.

A 1972 study by Morse et al described the epidemiology of the event:

Of 97 persons exposed, 90 were infected, 32 experienced typical icteric [jaundice] disease, 22 were anicteric but symptomatic, and 36 asymptomatic players were recognized as having significantly elevated serum glutamic pyruvic transaminase values (> 100 units). Other athletes, using the same facilities but arriving six days after the established date of exposure, were unaffected. The decision to obtain blood samples from the entire team, as soon as the initial cases were recognized, resulted in the demonstration of an unexpectedly high attack rate of 93% . . .

An attack rate of 93% is remarkable, but potentially consistent with a high inoculum that could have been delivered by contaminated water. Friedman et al returned to the event in a 1985 study. Using a radioimmunoassay to test stored serum samples for IgM antibody to hepatitis A virus, they found that

Only individuals with icteric hepatitis were found to have IgM anti-HAV in serum; those with presumed anicteric illness were shown not to be infected with hepatitis A virus. The attack rate was thus only 34%, not 93% as originally reported, and the incidence of icteric illness in those infected was 100%, not 33%.

What made the other players sick thus remains a mystery, though one can speculate about potential pathogens in the environment that could have contaminated the practice field faucet given the negative pressure scenario. I'm always intrigued by disease events that seem so open-and-shut based on the technology of one era but less so when analyzed with the technology of another. This is one of those events.

(image source: Wikipedia)